Taylor’s series theorem is a powerful mathematical tool that allows us to represent many different functions as an infinite sum of simpler functions. This theorem has many practical applications in science, engineering, and finance, among other fields.
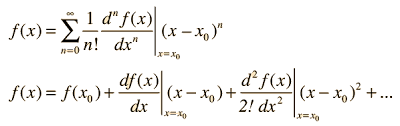
The theorem is named after the British mathematician Brook Taylor, who first discovered it in the early 18th century. Taylor’s series is a representation of a function as an infinite sum of terms that are determined by the function’s derivatives evaluated at a single point. The formula for Taylor’s series is given as:
f(x) = f(a) + f'(a)(x-a) + f”(a)(x-a)^2/2! + f”'(a)(x-a)^3/3! + …
where f(x) is the original function, a is a point around which the series is centered, and the terms in the sum involve the derivatives of the function evaluated at that point a. The factorial notation is used to simplify the expression of the higher order derivatives.
The Taylor’s series theorem is an extension of the simpler concept of a Taylor polynomial, which is a finite sum of terms obtained by truncating the infinite series at a certain degree. The Taylor polynomial approximates the original function within a certain interval around the point a.
The usefulness of Taylor’s series lies in the fact that many functions can be approximated well by a Taylor polynomial or series. For example, the sine, cosine, exponential, and logarithmic functions can all be expressed as Taylor series. This allows us to approximate the values of these functions to a high degree of accuracy, even if their original definition is very complex.
Moreover, Taylor’s series can be used to find derivatives of functions that are otherwise difficult to compute, such as implicit functions, transcendental functions, or solutions of differential equations. By approximating the function with a Taylor series, we can obtain a simplified expression for its derivative at a specific point.
There are several variations of Taylor’s series, such as the Maclaurin series, which is a special case of the Taylor series obtained by centering the series at a=0. The Maclaurin series is particularly useful when dealing with functions that are symmetric around the origin, such as the sine and cosine functions.
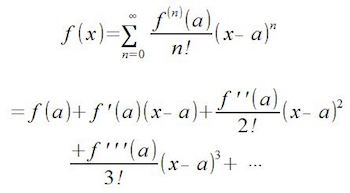
The convergence of Taylor’s series is an important issue to consider when using it for approximations. Some functions converge rapidly to their Taylor series, while others may converge slowly or not at all. The remainder term of the Taylor series can be used to estimate the error of the approximation and to determine how many terms of the series are needed to achieve a desired level of accuracy.
In conclusion, Taylor’s series is a powerful mathematical tool that has many applications in various fields of science and engineering. It allows us to approximate complex functions with simpler ones, to find derivatives of difficult functions, and to solve differential equations. While the convergence of Taylor’s series must be carefully considered, this theorem provides a valuable tool for many mathematical problems.
References:
- Stewart, J. (2015). Calculus: Early Transcendentals (8th ed.). Cengage Learning.
- Arfken, G. B., & Weber, H. J. (2013). Mathematical Methods for Physicists (7th ed.). Academic Press.
- Khan Academy. (n.d.). Taylor & Maclaurin series. https://www.khanacademy.org/math/ap-calculus-bc/bc-series-new/bc-10-11/v/taylor-maclaurin-series-intuition