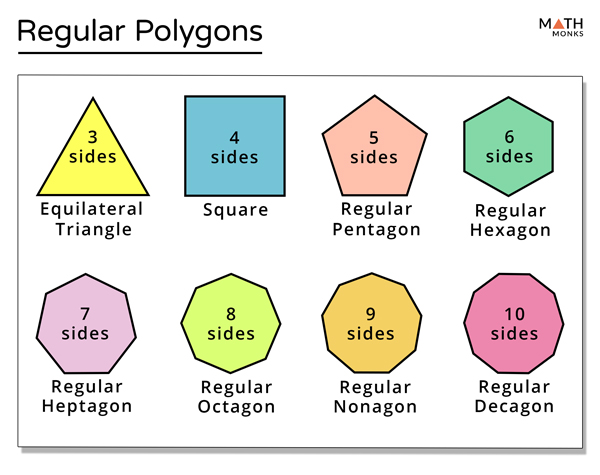
A polygonis a shape formed from three or more points joined by three or more straight lines, The points are known as vertices (each point is a vertex), and the lines are called sides—the name of most polygons relates to the number of angles or sides it has.